If F is Continuous and 08f X dx “19 Evaluate the Definite Integral
ELet p(x) be the antiderivative of a continuous function f(x) defined on [a, b] then, the definite integral of f(x) over [a, b] is denoted by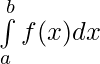 and is equal to [p(b) – p(a)].
and is equal to [p(b) – p(a)].
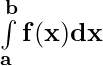 = P(b) – P(a)
= P(b) – P(a)
The numbers a and b are called the limits of integration where a is called the lower limit and b is called the upper limit. The interval [a, b] is called the interval of the integration.
Note
- Constant integration is not included in the evaluation of the definite integral.
-
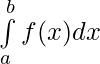 is read as "integral of f(x) from a to b"
is read as "integral of f(x) from a to b"
Steps to find Definite Integrals
To find the definite integral of f(x) over interval [a, b] i.e.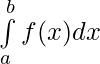 we have following steps:
we have following steps:

- Find the indefinite integral ∫f(x)dx .
- Evaluate P(a) and P(b) where P(x) is antiderivative of f(x), P(a) is value of antiderivative at x=a and P(b) is value of antiderivative at x=b.
- Calculate P(b) – P(a).
- The resultant is the desired value of the definite integral.
Definite Integrals by Substitution
For the integral![]() . Let g(x) = t, then g'(x) dx = dt where for x = a , t = g(a) and for x = b, t = g(b).
. Let g(x) = t, then g'(x) dx = dt where for x = a , t = g(a) and for x = b, t = g(b).
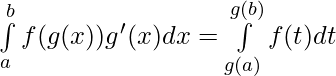
If the variable is changed in the definite integral then substitution of a new variable affects the integrand, the differential (i.e. dx), and the limits.
The limits of the new variable t are the values of t corresponding to the values of the original variable x. It can be obtained by putting values of x in the substitution relation of x and t.
Properties of Definite Integral
Property 1) 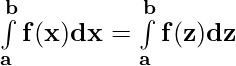
Proof:
Let p(x) be a antiderivative of f(x). Then,
{p(x)} = f(x) ⇒ \
{p(z)} = f(z)
= p(b) – p(a) ——————- (i)
and
= p(b) – p(a) ——————-(ii)
From (i) and (ii)
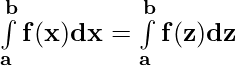
Property 2)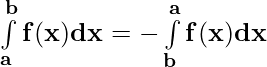
If the limits of the definite integral are interchanged then, its value changes by a minus sign only.
Proof:
Let p(x) be the antiderivative of f(x). Then,
= p(b) – p(a)
and
= -[p(a) – p(b)] = p(b) – p(a)
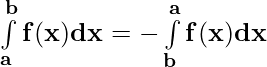
Property 3) 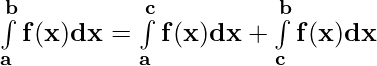 where a < c < b
where a < c < b
Proof:
Let p(x) be the antiderivative of f(x). Then,
= p(b) – p(a) ——————(i)
= [p(c) – p(a)] + [p(b) – p(c)] = p(b) – p(a) ——————(ii)
From (i) and (ii)
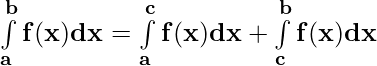
Property 4)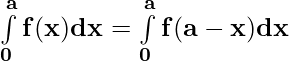
Proof:
Let x = a – t . Then, dx = d(a – t) ⇒ dx = -dt
When x = 0 ⇒ t = a and x = a ⇒ t = 0
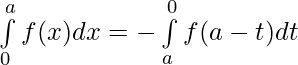
⇒
[ By second property ]
⇒
[ By first property ]
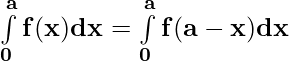
Property 5)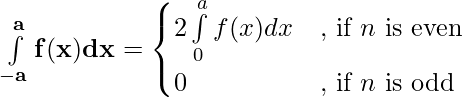
Proof:
Using third property
——————–(i)
Let x = – t , dx = -dt
Limits : x= -a ⇒ t = a and x = 0 ⇒ t = 0
[By second property]
⇒
[By first property] ———–(ii)
From (i) and (ii)
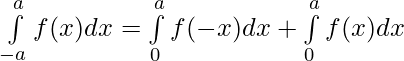
⇒
![Rendered by QuickLaTeX.com \int\limits_{-a}^{a}f(x)dx=\int\limits_{0}^{a}[f(-x)+f(x)]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-38c4aa3c932dced55a7e97fb2048cb8a_l3.png)
⇒
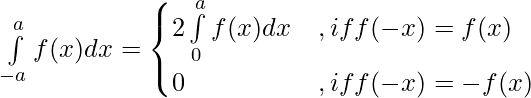
⇒
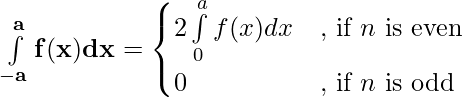
Property 6) If f(x) is a continuous function defined on [0, 2a],
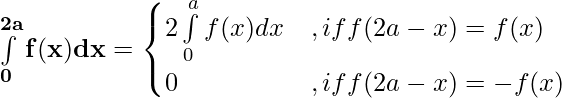
Proof:
Using third property
—————–(i)
Consider
Let x = 2a – t , dx = -d(2a – t) ⇒ dx = -dt
Limits : x= a ⇒ t = a and x = 2a ⇒ t = 0
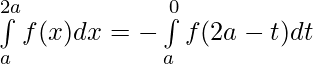
⇒
[ Using second property]
⇒
[ Using first property]
Substituting
in (i)
![Rendered by QuickLaTeX.com \int\limits_{0}^{2a}f(x)dx=\int\limits_{0}^{a}f(x)dx+\int\limits_{0}^{a}f(2a - x)dx = \int\limits_{0}^{a}[f(x) + f(2a - x)]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac9b1615132b60c21ccdf595faa34f2a_l3.png)
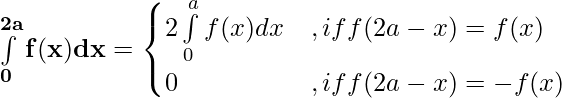
Property 7)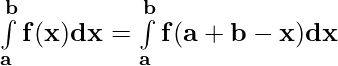
Proof
Let t = a + b – x ⇒ dt = -dx
Limits : x = a , y = b and x = b , y = a
After putting value and limit of t in
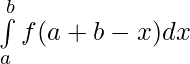
⇒
⇒
[Using second property]
⇒
[Using first property]
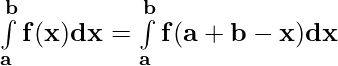
Solved Example on Definite Integrals
Problem 1: Evaluate:
(i) 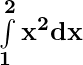
(ii) 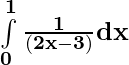
(iii) 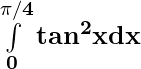
Solution:
(i)
=
= [23 – 13]
= 8 – 1
dx = 7
(ii)
=
= (1/2)[log|-1| – log|-3| ]
= (1/2)[ log 1 – log 3]
= (1/2)[0 – log 3]
= (1/2)log 3
(iii)
=
(sec2 x – 1) dx
=
= [tan(π/4) – (π/4)] – [tan 0 – 0 ]
= 1 – (π/4)
Problem 2: Evaluate: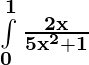
Solution:
Let 5x2 + 1 = t. Then, d(5x2 + 1) = dt ⇒ 10 x dx = dt
For limits : Lower limit ⇒ x = 0 then t = 5x2 +1 = 1 and Upper limit ⇒ x = 1 then t = 5x2 + 1 = 6
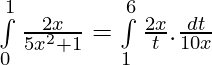
=
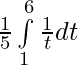
=
![Rendered by QuickLaTeX.com \frac{1}{5}\big[log\hspace{0.1cm}t\big]_1^6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-095600c8f792450ef6b4c478545b1a42_l3.png)
= (1/5) [log 6 – log 1]
= (1/5) log 6
Problem 3: Evaluate : 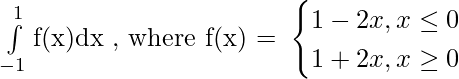
Solution:
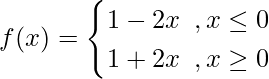
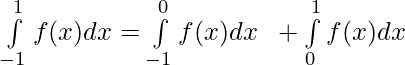
[Using definition of f(x)]
![Rendered by QuickLaTeX.com \int\limits_{-1}^{1} f(x) dx = \big[x-x^2\big]_{-1}^0 \hspace{0.2cm}+ \big[x + x^2\big]_{0}^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f69167be35944287458f950f562c149_l3.png)
= [0 – ( -1 – 1)] + [(1 + 1) – (0)]
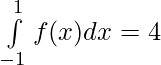
Problem 4: Evaluate: 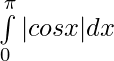
Solution:
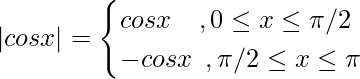
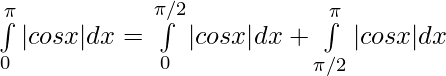
⇒
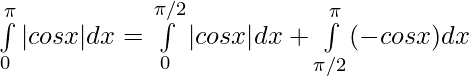
⇒
![Rendered by QuickLaTeX.com \int\limits_0^\pi|cos x| dx = \big[cos x\big]_0^{\pi/2} - [sin x\big] _{\pi/2}^\pi](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6b0a51637020c20901e20d047a615af7_l3.png)
= 1 + 1
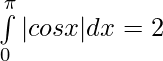
Problems 5: Evaluate: 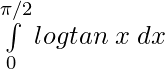
Solution:
I =
———————(i)
I =
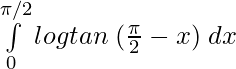
Using
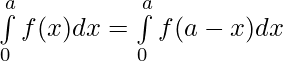
I =
——————-(ii)
Adding (i) and (ii)
2I =
![Rendered by QuickLaTeX.com \int\limits_0^{\pi/2}[log \hspace{0.1cm}tanx\hspace{0.1cm} +log \hspace{0.1cm}cotx\hspace{0.1cm}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dab7c2b87ed309bb305ccf7a08ea57c4_l3.png)
2I =
![Rendered by QuickLaTeX.com \int\limits_0^{\pi/2}[log \hspace{0.1cm}(tanx\hspace{0.1cm} cotx)\hspace{0.1cm}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-791ce23884e054b9d9301ddbaad2d641_l3.png)
2I =
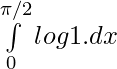
2I =
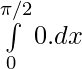
I = 0
Problem 6 : Evaluate : 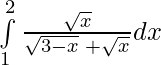
Solution:
I =
—————–(i)
Using property
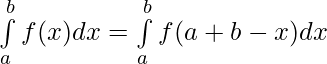
I =
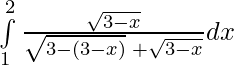
I =
—————(ii)
Adding (i) and (ii)
2I =
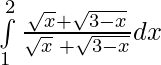
2I =
2I = 2 – 1
2I = 1
I = 1/2
FAQs on Definite Integrals
Question 1: What is meant by definite integrals?
Answer:
Definite integrals are integrals that are defined under proper limits i.e. their upper and lower limits are specified. It is represented as ∫b a f(x) dx where a is the upper limit and b is the lower limit of integration.
Question 2: How are definite integrals simplified?
Answer:
For simplifying definite integrals use the following steps:
- Simplify the integral normally.
- Substitute upper and lower limits to the answer of integration.
- Subtract both the answer obtained in step 2
Question 3: Write the formula for solving definite integrals.
Answer:
Suppose a definite integral of a function f(x) in the interval [a, b] is required, then,
∫b a f(x) dx = F(a) – F(b)
where, ∫ f(x) dx = F(x) + C
Question 4: What does the value obtained from solving definite integral represent? Can it be negative?
Answer:
The value obtained from solving the definite integral represents the area. Yes, it can also be negative.
Source: https://www.geeksforgeeks.org/calculate-definite-integral/
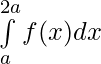
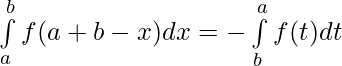
![Rendered by QuickLaTeX.com \int\limits_1^21.dx =\big[x\big]_1^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72d41902dd0b3f564c46081cb922a1c7_l3.png)
0 Response to "If F is Continuous and 08f X dx “19 Evaluate the Definite Integral"
Post a Comment